
在上一篇文章中,我們學會了 Monad 的實用工具 chain,它透過結合 map 和 join 來解決巢狀容器問題,讓我們的函數組合保持流暢。今天會再更深入認識 Monad,瞭解它到底是什麼、以及它需要遵守哪些重要定律。
一個型別若同時提供
of與chain,並且滿足 Monad 的三條定律(結合律、左右單位律),那它就是 Monad。
我們可以從三個角度來理解 Monad,分別回答 What、How、Why 這三個問題。
map 然後 join (壓平) 來達成chain 的魔法 (map + join)chain 看似神奇,但它的內部機制非常簡單。它其實就是我們上一篇文章手動操作的組合:map 加上 join。
// 以 m 為某個 monad 值,且 f 函數簽章是 a -> M(b)
m.chain(f) === m.map(f).join()
這解釋了 Monad 在結構上(What)和機制上(How)的行為:
map(f):chain 首先會像 map 一樣,將我們提供的函數 f 應用到容器內的值上。這也解釋了結構問題的來源:當 f 回傳一個容器時,map 會把它包起來,產生 Maybe(Maybe(address)) 這種「盒子裡的盒子」。join():收到「盒子裡的盒子」後,chain 會再執行 join (也常被稱為 flatten)。join 的功能很單純,就是將任何兩層相同類型的巢狀容器壓平一層:M(M(a)) -> M(a)。它就像是剝掉洋蔥最外層的那一層皮,或從一個箱子裡拿出內部的箱子。簡言之,chain 的完整流程是:先用 map 創造出巢狀結構,然後立刻用 join 將其撫平,變回單層結構,為下一次的 chain 操作做好準備。
在先前 Functor 的文章中曾提過,可以將程式設計中的每個型別都視為擁有自己的世界/集合,大方向又可分為一個「一般值的世界」和一個「容器值的世界」。
Functor 的 map 讓我們能留在容器世界中。map 就像一座橋樑,將一個存在於「一般世界」的函數 (a -> b) 提升 (lift) 到「容器世界」來操作,讓我們可以對容器內的值進行轉換,而結果依然被安全地包裹在同一個容器中 (M(a) -> M(b))。
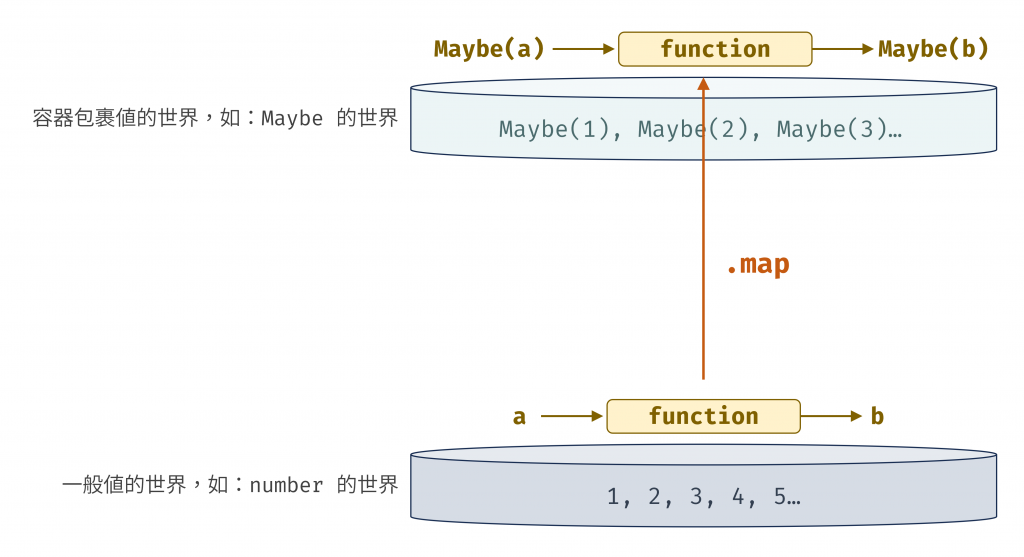
圖 1 Functor 的 map 將一個存在於「一般世界」的函數 (a -> b) 提升 (lift) 到「容器世界」來操作,讓我們可用 M(a) -> M(b) 來操作(資料來源: 自行繪製)
但我們遇到的新問題是:有些函數天生就是「跨界」的。它們接收一個「一般世界」的值,卻回傳一個「容器世界」的值,例如我們上一篇文章的 safeProp('addresses') 會收到一個物件作為輸入、回傳 Maybe 作為輸出。這種函數的簽章是 a -> M(b)。
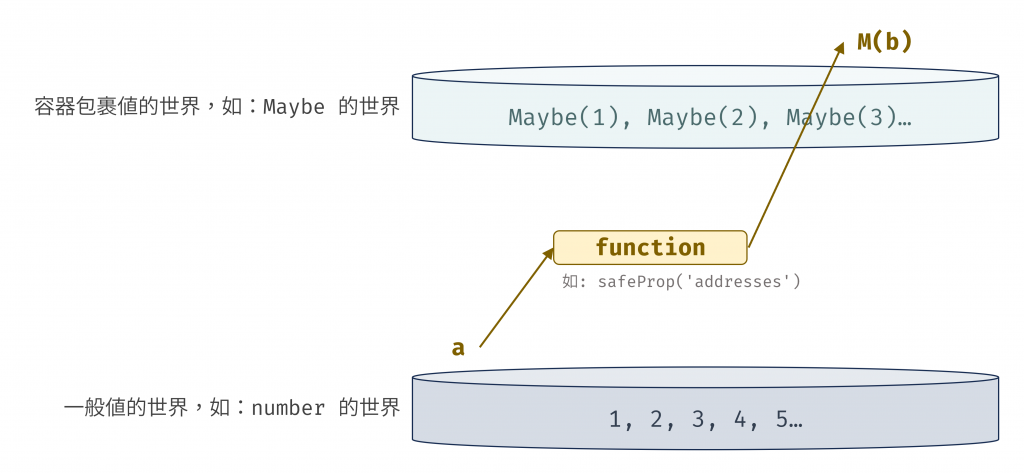
圖 2 有些「跨界」的函數會接收一個「一般世界」的值,回傳一個「容器世界」的值(資料來源: 自行繪製)
如果我們用 map 這座為「一般世界」函數設計的橋樑,去承載一個本身就會「跨界」的函式,就會導致混亂——也就是我們看到的 Maybe(Maybe(address)) 巢狀結構。
Monad 的 chain (或 bind) 正是為了解決這個問題而生的工具。它的作用是:取一個「跨界」函數 (a -> M(b)),並將它「綁定」(bind) 到容器世界的流程中,讓整個操作的起點和終點都維持在容器世界內 (M(a) -> M(b))。它巧妙地處理了跨界函數所創造的新容器,將其與現有容器融合,進而撫平了巢狀結構。
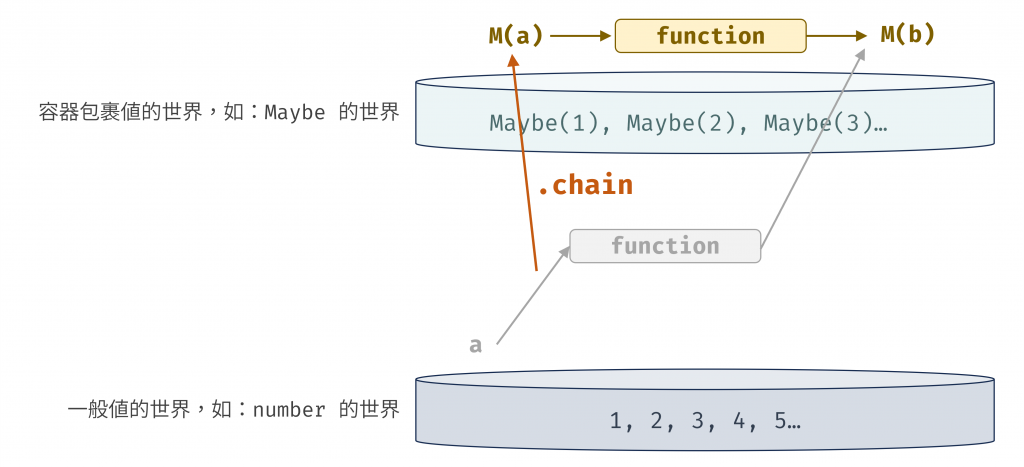
圖 3 chain 將跨界函數綁定到容器世界的流程中(資料來源: 自行繪製)
map 與 chain那我們何時要用 map,何時要用 chain 呢? 使用情境取決於想要應用的函數簽章 (function signature)。
| 方法 | 用途 | 接受的函數簽名 | 結果型別 |
|---|---|---|---|
map |
將一個普通函數應用到容器內的值上。 | a → b |
M(b) |
chain |
將一個回傳新容器的函數應用到容器內的值上。 | a → M(b) |
M(b) |
當我們的轉換函式很單純,只是 value -> newValue,就用 map。
當轉換函式本身帶有 context,可能會失敗、有副作用或非同步,因此回傳一個新的容器 value -> M(newValue),就要用 chain 來保持組合鏈的順暢。
有人可能會聽過一種說法:「Monad 是一種處理副作用的方式。」這說法沒有錯,但實際上 Monad 的抽象本質與「副作用」本身無關。它只是一個通用機制,讓我們能安全地組合那些「帶有特定上下文(context)」的計算。
為了管理副作用,Monad 採用了一種特殊的方法:它將一個會產生副作用的行為(如讀取檔案、印出訊息),從一個立即執行的動作,轉變為一個被包裹在容器中的值,例如 IO(() => 檔案內容)。這種做法延遲了副作用的執行,讓我們能在純函數的世界中安全地傳遞、處理這些「代表著副作用」的值。
接著,我們就能利用 chain 這個工具,將這些有依賴關係的計算串連起來。chain 確保了後面的計算,會在前面計算完成並提供結果後才執行,同時維持整個處理流程的扁平與一致。
只不過,在許多常見的 Monad 類型中,這個 context 恰好就是有副作用的同步任務(如 IO)或非同步任務(如 Task),所以我們才會看到 Monad 經常與副作用綁在一起。但 Monad 的真正力量在於它的組合性,能夠讓任何「會回傳容器的函式」流暢地串接起來,而副作用剛好是其中一個被解決的應用場景。
chain 的根本性chain 是由 map 和 join 推導出來的,但其實反過來 map 和 join 也可以由 chain 推導出來。
chain 推導 mapm.map(f) 等價於 m.chain(x => M.of(f(x)))。
我們用 chain 來應用一個函式,但因為 f(x) 回傳的是一個普通值,我們必須手動用 M.of 把它包回容器中,以滿足 chain 對回傳值(容器包裹值)的要求。而這結果就和 m.map(f) 應用值再包回容器的結果相同。
chain 推導 joinm.join() 等價於 m.chain(id) (其中 id = x => x)。
當 m 是一個 M(M(a)) 時,m.join() 會攤平一層得到 M(a);而 chain 會取出內部的 M(a) 並將其交給 id 函式。id 函式什麼都不做,直接回傳這個 M(a)。因為 chain 會自動壓平,所以最終結果就是單層的 M(a)。
由此可知,只要一個型別實作了 of 和 chain,並遵守 Monad 定律,它就自動具備了 map 和 join 的能力,是一個 Monad、也會是個 Functor。
回顧一下之前介紹的 Maybe、Either、IO、Task 等資料類型,我們會發現,它們不僅僅是 Functor,其實也都是 Monad。
chain 很適合用來串接一系列可能失敗的屬性存取chain 和 Maybe 類似,可處理線性的短路邏輯chain 用於串接有依賴關係的副作用。IO 的 join 代表執行一個會「回傳另一個 IO 動作」的 IO
const fs = require('fs')
const compose = (...fns) => x => fns.reduceRight((v, f) => f(v), x)
class IO {
static of(x) {
return new IO(() => x); // 延遲執行,避免立刻求值產生副作用,在真正呼叫之前,無法知道 x 的值
}
constructor(fn) {
this.unsafePerformIO = fn; // value 是一個函式,一個會延遲執行的函式
}
map(fn) {
return new IO(compose(fn, this.unsafePerformIO)); // 透過 compose 組合新的函式 fn 和現有的值 $value
}
// 為 IO 多定義 join 和 chain 方法
chain(fn) {
return this.map(fn).join();
}
join() {
return new IO(() => this.unsafePerformIO().unsafePerformIO()); // 這裡的 join 不是「立刻『執行副作用』兩次」,而是把兩層描述合併為一層描述;真正的副作用仍在最終呼叫 unsafePerformIO() 才發生
}
}
// 假設 readFile 和 log 都是回傳 IO 的函式
const readFile = (filename) => new IO(() => fs.readFileSync(filename, 'utf-8'));
const log = (content) => new IO(() => { console.log(content); return content; });
// 定義主程式:讀取設定檔,然後將其內容印出。第二個動作依賴於第一個動作的結果。
const program = readFile('config.json').chain(log);
program.unsafePerformIO(); // 執行主程式
chain 方法和 Promise.then 有點類似。不過 Promise 一旦建立就會立即執行,Promise.then 比較像是為一個「已經在運行的」任務安排後續,並傳遞它「已完成的結果」。相反地,Task 只是一個描述未來任務的藍圖。所以 Task.chain 是在組合、串接多個「尚未開始的」任務藍圖。每一次 chain 都是在為這份總藍圖增加一個新的步驟。由上可知,Monad 不是特定於 Maybe 的專利,而是一個通用的抽象模式,用來在任何給定 context 中,對有依賴關係的計算進行排序。
無論 context 是「值的缺席」(Maybe)、「可能的錯誤」(Either)、「副作用」(IO)還是「非同步」(Task),串接它們的機制(chain)都是一樣的。Monad 提供了一個統一的 API,讓我們能夠說:「先做這件事,然後根據它的結果,再做下一件事。」
就像 Functor 有自己的定律一樣,Monad 也有自己的定律。這些定律確保 chain 的行為可預測,讓我們能安心地用它建構複雜流程。也可以把這些規則視為把「Monoid 的組合精神」搬到「帶脈絡的計算步驟」上:在 Monoid 我們組合同型別世界的值(滿足結合律與單位元素);在 Monad 我們組合計算的步驟(滿足結合律與左右同一律)。
M.chain(f).chain(g)必須等價於M.chain(x => f(x).chain(g))
假設 f 函數簽章是 a -> M(b),g 函數簽章是 b -> M(c),來拆解一下流程:
M 執行 chain(f),chain 會先用 .map(f) 得到 M(M(b)),然後再用 join 攤平得到 M(b)
chain(g),一樣先用 .map(g) 得到 M(M(c)),然後用 join 攤平得到 M(c)
M(c)
f 再做 g」這整段流程,寫成一個大函數:
x => f(x).chain(g)
x => f(x).chain(g) 的函數簽章是 a -> M(c),我們也可以視為有個 e 函數,e 的函數簽章是 a -> M(c)
M 一次性 chain 上去,也就是說 M.chain(x=>f(x).chain(g)) 等於 M.chain(e),會先 .map 得到 M(M(c)),然後用 join 攤平得到 M(c)
M(c)
左右兩邊結果都是 M(c),因此兩個運算方式等價。
這就像三個步驟的工作流程,不管是「分兩次做」還是「包成一個大流程一次做」,結果都相同。
join 來理解結合律因為 chain 可以拆成 map 和 join,所以同樣的 chain 結合律規則也可以寫成:
compose(join, map(join))必須等價於compose(join, join)
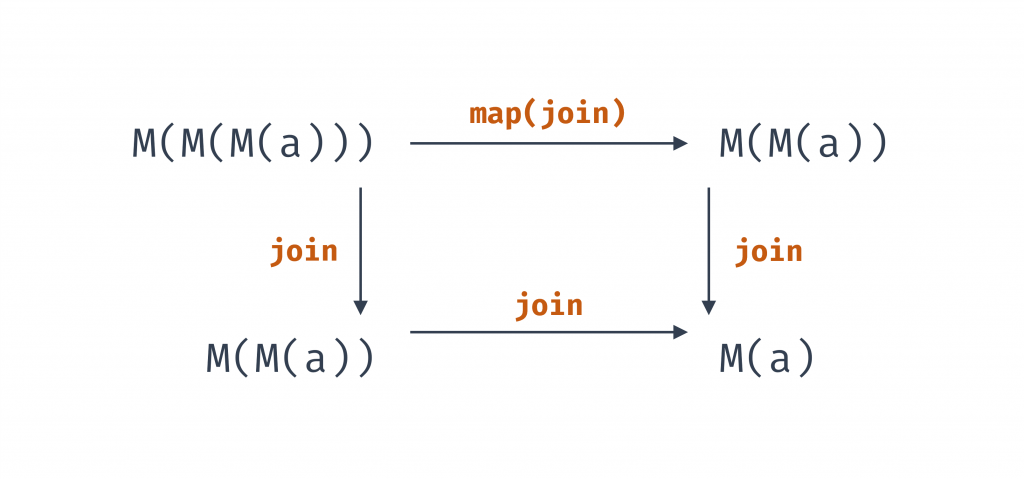
圖 4 用 join 來理解結合律(資料來源: 自行繪製)
如上圖,對於三層容器 M(M(M(a))) 來說:
map(join) 把內層合併成 M(M(a)),再 join 成 M(a)
join 外層成 M(M(a)),再 join 成 M(a)
最後結果會相同。
補充,不過中間的步驟 map(join) 不等於 join 的結果,兩條路徑的中途節點可能不同,但最終結果一樣。
Monad 有兩個方向的 Identity 定律,它們確保 of 作為「最小脈絡」的行為是無害的。
以下一樣假設 f 函數簽章是 a -> M(b)。
左單位元 (Left Identity)
M.of(a).chain(f)必須等價於f(a)
M.of(a) 會先把值 a 放進容器,接著 .chain(f) 會呼叫 f,得到一個新的容器 M(b),這結果等於直接呼叫 f(a) 得到 M(b)。
舉例程式如下:(完整程式可見連結)
const f = (x) => Maybe.of(x + 1);
const result1 = Maybe.of(5).chain(f); // result1 是 Just(6)
const result2 = f(5); // result2 也是 Just(6)
// 兩個結果相同
右單位元 (Right Identity)
M.chain(M.of)必須等價於M
如果容器裡的值只是被 of 再包一層,最後被 chain 壓平後,還是原來的容器。
舉例程式如下:(完整程式可見連結)
// M.chain(M.of) === M
const m = Maybe.of(5);
const result1 = m.chain(Maybe.of); // result1 是 Just(5)
const result2 = m; // result2 也是 Just(5)
// 兩個結果相同
join 來理解同一律
compose(join, of)必須等價於compose(join, map(of))必須等價於id
以程式來看就是compose(join, of) === compose(join, map(of)) === id;
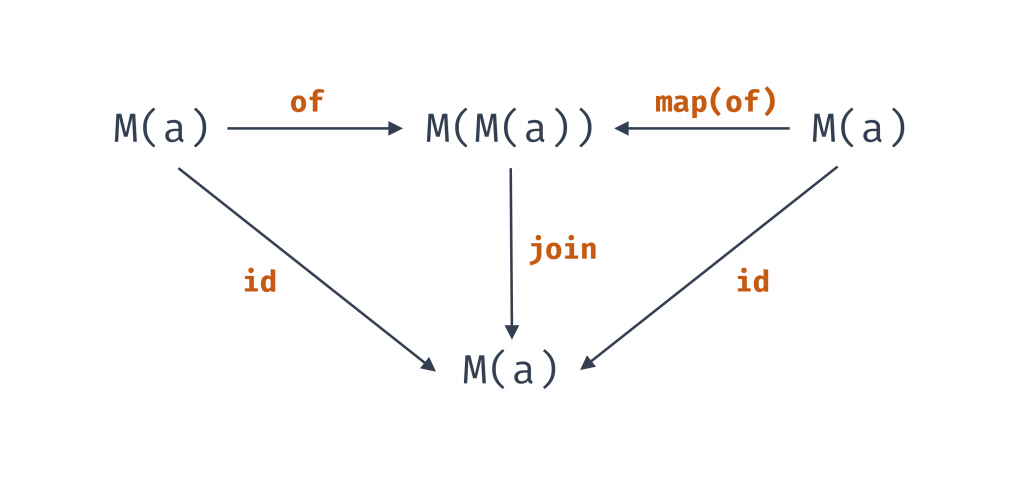
圖 5 用 join 來理解同一律(資料來源: 自行繪製)
如上圖:
M(a) 出發,不管是走「先 of 再 join」或「直接 id」,最後結果一樣map(of) 再 join」或「直接 id」結果也一樣of 就像透明膠膜,把東西套一層再拆掉,內容完全沒變。
Monad 的定律和 Monoid 看起來非常相似,都是結合律和同一律,其實兩者的關係在數學的範疇論(Category Theory)中有一個更精確的說法:
Monad 是「在 Endofunctor 範疇上的 Monoid」(Monad is a Monoid in the Category of Endofunctors)
這句話聽起來很嚇人,但它的意思就是:Monad 和 Monoid 都是描述「可組合性」的抽象模式,只是它們組合的對象不同。
有一個集合 A 和一個二元運算 •,它能將兩個同類型的值組合成另一個同類型的值。
例如數字加法、字串串接。它必須滿足:
(a • b) • c = a • (b • c)
e,使得 a • e = a = e • a
在 Monad 裡,元素換成了「帶有 context 的計算」(也可想成帶有容器的計算)。
具體來說,若有一個函式 a -> M(b) 和另一個函式 b -> M(c),我們希望能將它們組合成 a -> M(c)。這種組合方式稱為 Kleisli composition,而 chain 就是用來完成這件事的二元運算。
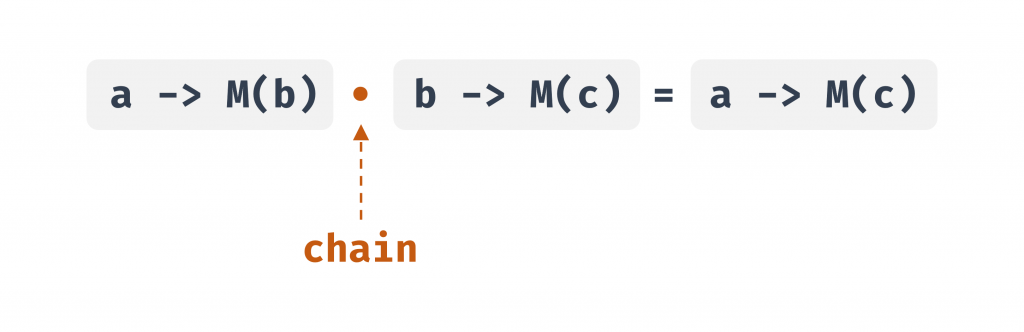
圖 6 chain 可組合 a -> M(b) 和 b -> M(c) 這兩個函數,得到 a -> M(c) (資料來源: 自行繪製)
同樣地,它也需要滿足兩個規則:
m.chain(f).chain(g) === m.chain(x => f(x).chain(g))
M.of 扮演「中性」角色,M.of(a).chain(f) === f(a),m.chain(M.of) === m
chain 就像 Monoid 的二元運算 •,用來將計算步驟一個接一個串起來;而 of 則像 Monoid 的單位元 e,是一個「無害的步驟」,插入計算鏈中不會改變結果。
簡言之,Monoid 在組合「值」,而 Monad 在組合「計算」。它們本質上遵循著同樣的結合律與單位元精神,讓我們能在 FP 世界裡安全地構建運算流程。
簡單列一下 Monad 的優點與限制,理解它的優缺點,能幫助我們在正確的情境下運用它。
chain 這個統一的 API,用來串接那些會回傳容器的函式,避免了 Maybe(Maybe(x)) 這類巢狀結構,讓函式組合鏈保持扁平,提升可讀性。chain 能避免常見的 Callback Hell 或 Promise Pyramid of Doomof 方法,Monad 允許我們對容器內的值進行操作,也提供了一種信任機制:我們知道值從容器取出後,最終會被 of 重新包裝回容器中,確保計算的脈絡 (context) 不會遺失chain (序列執行) 會變得不方便。這類情境更適合使用 Promise.all 或其他專門的並行處理機制Either) 在遇到第一個錯誤 (Left) 時就會停止整個計算鏈。它們不適合用於需要一次性檢查所有錯誤並回報的驗證流程。這時可能要使用其他工具來解決,這類工具會在後續文章介紹。用幾個問題統整昨天和今天的文章。
當我們使用 .map 來處理一個本身就會回傳容器的函式時(例如,一個可能失敗的函式 a -> Either(b)),我們會得到像 Either(Either(Either(b))) 這樣難以操作的深層巢狀容器。
這種巢狀結構會打斷我們流暢的函式組合鏈,迫使我們寫出笨拙、命令式的程式碼來手動拆解容器。
對 FP 來說,能夠順暢且安全自在地組合函數是關鍵,巢狀容器讓我們無法順暢的組合函數,因此我們需要一種方法來解決這問題。
.map 來組合函數,當遇到會回傳容器的函數時,會導致程式碼出現巢狀結果,需要手動呼叫 join 來壓平 (map(f).join()),不斷重複相似的程式碼,讓程式變得累贅。chain 來處理這些函式,將 map 和 join 合併為一個操作。讓我們能將多個有依賴關係的計算,串接成一個扁平、線性、且極易閱讀的序列 (m.chain(f).chain(g))。join 方法) 的 Pointed Functor (有 of 方法)。chain 方法的 Functor,而 chain 的行為等同於先 map 後再 join。map 是將「一般世界」的函數提升到「容器世界」的工具,那麼 chain 就是將一個從「一般世界」跨界到「容器世界」的函數綁定到容器世界流程中的工具。chain),用來排序那些依賴於前一個操作結果的計算,特別是當這些計算本身也會創造新脈絡時。